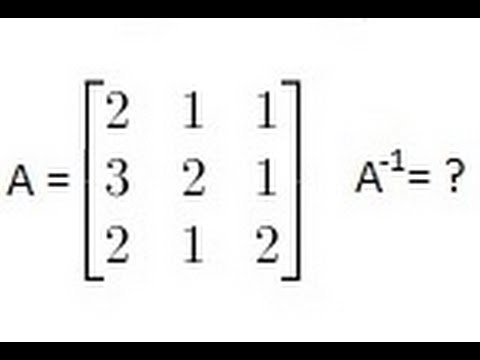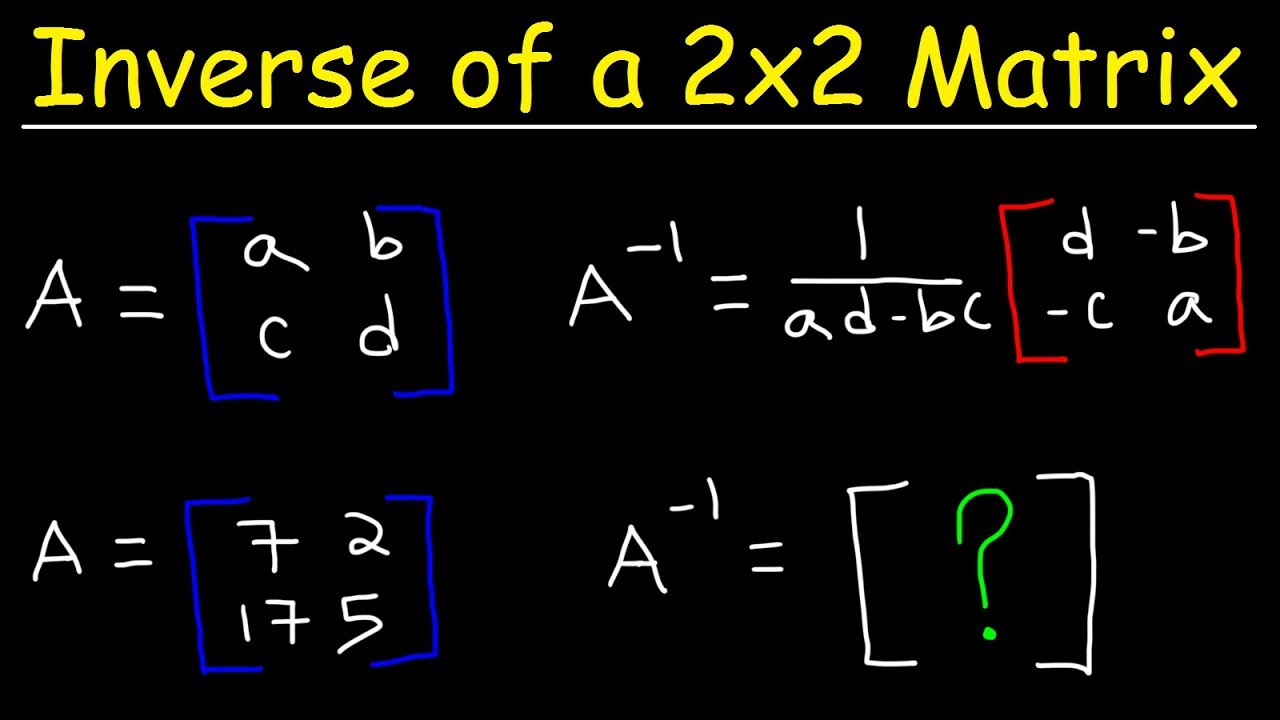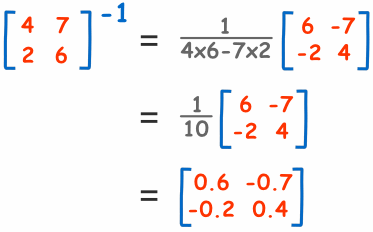Brilliant Strategies Of Tips About How To Find Out The Inverse Of A Matrix

The easiest way to determine the invertibility of a matrix is by computing its determinant: We must first insert matrix a into the excel sheet, as shown in the figure below. All you need to do now, is tell the calculator what to do with matrix a.

how to lose that double chin how to find out your wireless connection password how to increase ejaculation how to draw a anime body how to get rid of bone spurs how to protect my identity how to draw rectangles in photoshop how to fix a bricked psp

Inverse Matrix - Definition, Formulas, Steps To Find Inverse Matrix, Examples

Inverse Matrix - Definition, Formulas, Steps To Find Matrix, Examples

Inverse Of A 3x3 Matrix - Youtube

Algebra - Finding The Inverse Of A Matrix (1 Of 2) A 3X3 Matrix - Youtube

Algebra - Finding The Inverse Of A Matrix (1 2) 3x3 Youtube

3 Ways To Find The Inverse Of A 3x3 Matrix - Wikihow

Inverse Of A 2x2 Matrix - Youtube

Learn To Find The Inverse Of A 3x3 Matrix | Step-by-step Tutorial - Youtube

We can calculate the inverse of a matrix by:

How to find out the inverse of a matrix. Multiply 1/det(a) with adjoint of a (adj a) to get the inverse matrix of a. Inverse of a matrix is an important operation in the case of a square matrix. The key thing to note is that a matrix only has an inverse if its determinant does not equal 0.

The inverse of matrix a can be found using the formula given below. In other words, ai = ia = a. A matrix that has no inverse is.

Inverse of a matrix formula. We will find inverse of a matrix using the adjoint of matrix in the next section. For this, we need to calculate the determinant of the given matrix.

Press the inverse key [ x − 1] and press enter. Swap the positions of a and d, put negatives in front of b and c, and divide everything by ad−bc. So if a is a matrix, the inverse.

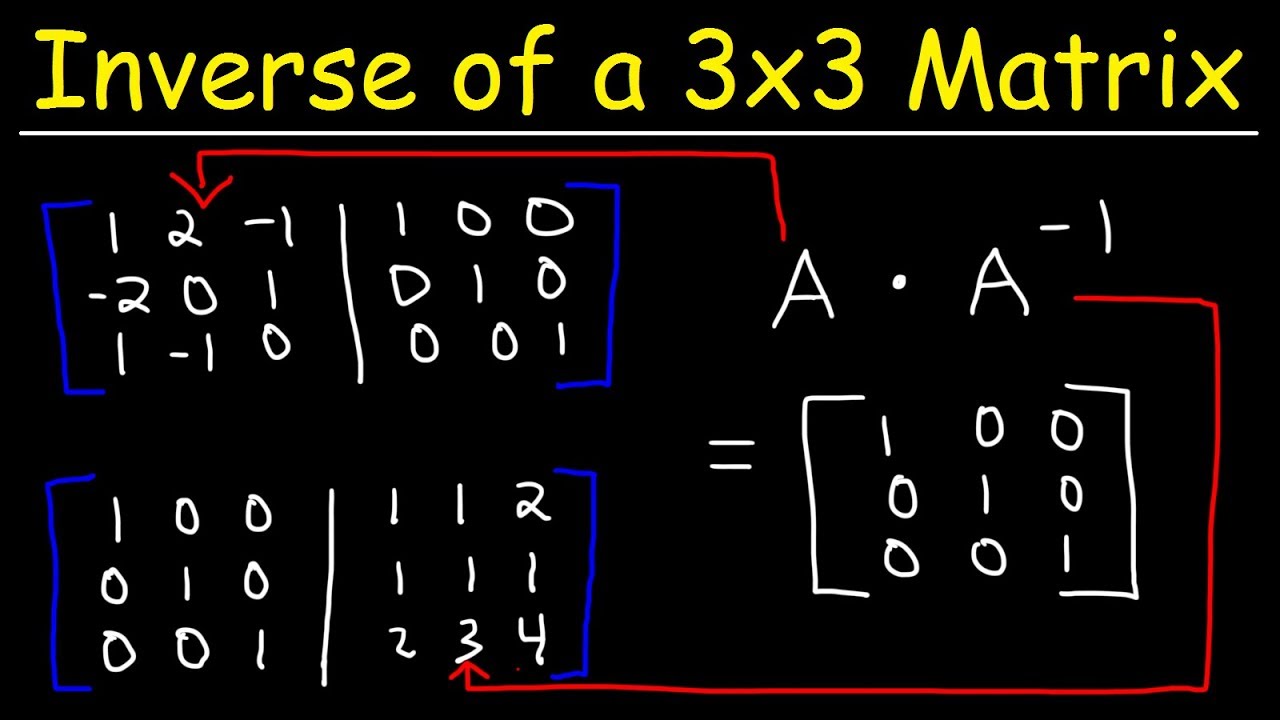
The inverse of a matrix a is the matrix b, such that ab = ba =. When we'll divide the adjugate or adjoint matrix of the given square matrix by the determinant of the matrix, we'll get the exact value of the inverse matrix. Just the same, for any n x n matrix a, multiplying a by the identity matrix i will give you a.

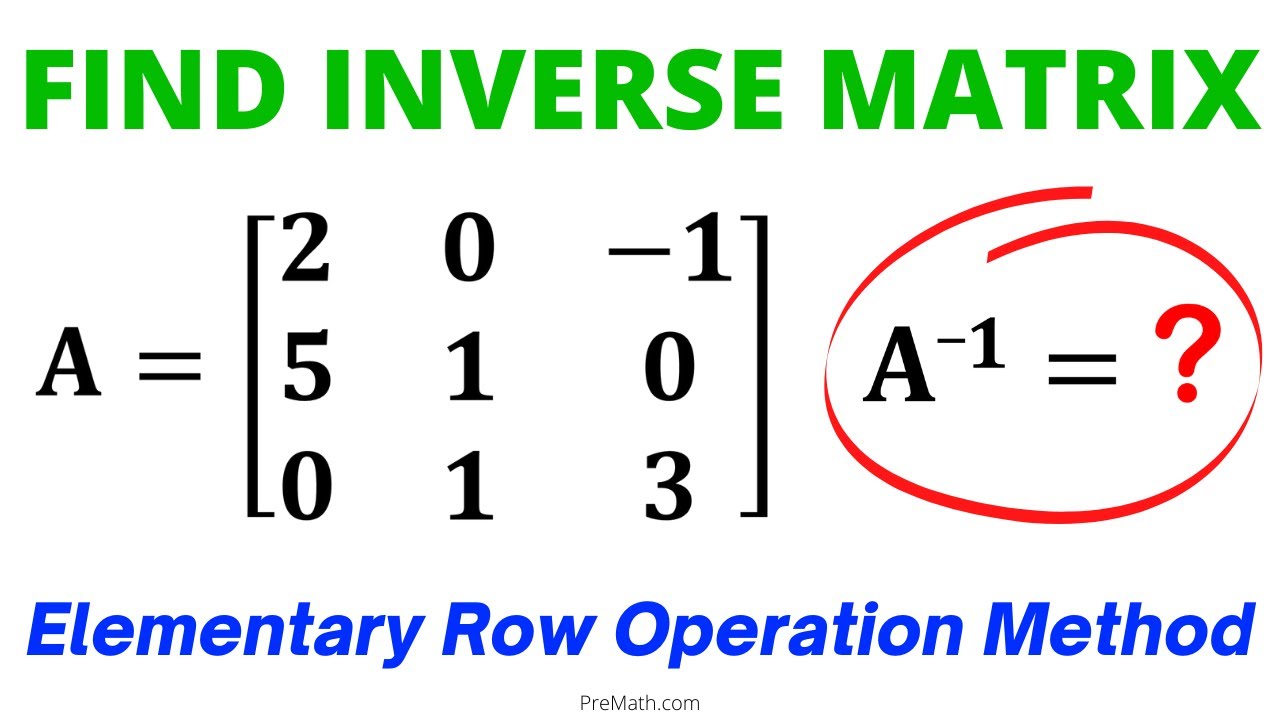
First we must find the inverse of matrix,. Details of how to find the determinant of a matrix can be seen here. The identity matrix that results will be.